Question

Q8. Look at the image.

Answer 1

Option B

Explanation:

Quadratic equation given in the question is,

`x^2+4x+2=0`

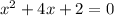
By comparing this equation with the standard quadratic equation,

`ax^2+bx+x=0`

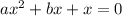
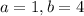`a=1,b=4` and
`c=2`

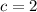
By using quadratic formula to get the roots of the given quadratic equation,

`x=(-b\pm√(b^2-4ac))/(2a)`

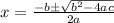
By substituting the values of a, b and c in the formula,

`x=(-4\pm√(4^2-4(1)(2)))/(2(1))`

`x=(-4\pm√(16-8))/(2)`

`x=(-4\pm√(8))/(2)`

`x=(-4-√(8))/(2),(-4+√(8))/(2)`

`x=-3.414,-0.5857`

`x=-3.41,-0.59`

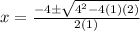
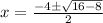
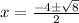
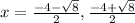
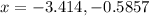
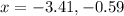
Therefore, Option B will be the answer.