Question

Two vehicles A and B accelerate uniformly from rest.

Vehicle A attains a maximum velocity of 30ms - in los
while B attains a maximum velocil) ol 40ms in the same
time. Both vehicles maintain these velocities for 6s belore
they are decelerated to rest in 6s and 4s respectively
Sketch on the same axes, velocity time graphs
for the motion of the vehicles
Calculate the velocity of each vehicle 18s aftur
the start. (VA
= 20ms -land vs
and vs = 20ms-')
How far will the two vehicles be from one
another during the moment in (ii) above?
(SA = 380m and SB
= 500m: SAB
120m). plz help​

Answer 1

(i) Please find attached the required velocity time graphs plotted with MS Excel

(ii) The velocity of vehicle A at the 18th second = 20 m/s

The velocity of vehicle B at the 18th second = 0 m/s

(iii) The distance between the two vehicles at the moment in (ii) above is 60 meters

Step-by-step explanation:

The given parameters of the motion of vehicles A and B are;

The acceleration of vehicles A and B = Uniform acceleration starting from rest

The maximum velocity attained by vehicle A = 30 m/s

The time it takes vehicle A to attain maximum velocity = 10 s

The maximum velocity attained by vehicle B = 30 m/s

The time it takes vehicle B to attain maximum velocity = The time it takes vehicle A to attain maximum velocity = 10 s

The time duration vehicle A maintains its maximum velocity = 6 s

The time duration vehicle B maintains its maximum velocity = 4 s

(i) From the question, we get the following table;

`\begin{array}{ccc}Time &V_A&V_B\\0&0&0\\10&30&40\\14&30&40\\16&30&20\\18&20&0\\22&0&\end{array}`

From the above table the velocity time graphs of vehicles A and B is created with MS Excel and can included here

(ii) The velocity of vehicle A at the start = 0 m/s

After accelerating for 10 seconds, the velocity of vehicle A = The maximum velocity of vehicle A = 30 m/s

The maximum velocity is maintained for 6 seconds which gives;

At 10 s + 6 s = 16 s, the velocity of vehicle A = 30 m/s

The time it takes vehicle A to decelerate to rest = 6 s

The deceleration of vehicle A,
`a_A` = (30 m/s - 0 m/s)/(6 s) = 5 m/s²

Therefore, we get;

v = u -
`a_A`·t

At the 18th second, the deceleration time, t = 18 s - 16 s = 2 s

u = 30 m/s

∴ v₁₈ = 30 - 5 × 2 = 20

The velocity of vehicle A at the 18th second,
`V_(18A)` = 20 m/s

For vehicle B, we have;

At the 14th second, the velocity of vehicle B = 40 m/s

Vehicle B decelerates to rest in, t = 4 s

The deceleration of vehicle B,
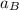`a_B` = (40 m/s - 0 m/s)/(4 s) = 10 m/s²

For vehicle B, at the 18th second, t = 18 s - 14 s = 4 s

∴
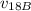`v_(18B)` = 40 m/s - 10 m/s² × 4 s = 0 m/s

The velocity of the vehicle B at 18th second,
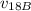`v_(18B)` = 0 m/s

(iii) The distance covered by vehicle A up to the 18th second is given by the area under the velocity-time graph as follows;

The area triangle A₁ = (1/2) × 10 × 30 = 150

Area of rectangle, A₂ = 6 × 30 = 180

Area of trapezoid, A₃ = (1/2) × (30 + 20) × 2 = 50

The distance covered in the 18th second by vehicle
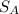`S_A` = A₁ + A₂ + A₃

∴
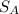`S_A` = 150 + 180 + 50 = 380

The distance covered in the 18th second by vehicle
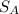`S_A` = 380 m

The distance covered by the vehicle B in the 18th second is given by the area under the velocity time graph of vehicle B as follows;

Area of trapezoid, A₅ = (1/2) × (18 + 4) × 40 = 440

The distance covered by the trapezoid,
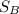`S_B` = 440 m

The distance of the two vehicles apart at the 18t second,
`S_(AB)` =
`S_B` -
`S_A`

∴
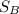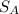
`S_(AB)` = 440 m - 380 m = 60 m

The distance of the two vehicles from one another at the 18th second,
`S_(AB)` = 60 m.