Question

isaac invested $77,000 in an account paying interest rate of 4.6% compounded continuously. Assuming no deposits or withdrawals are made, how much money, to the nearest cent, would be the count after 12 years?

Answer 1

$133,728 would be in the count after 12 hours.

Explanation:

Continuous compounding:

The amount of money, in continuous compounding, after t years, is given by:

`P(t) = P(0)e^(rt)`

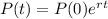
In which P(0) is the initial deposit and r is the interest rate, as a decimal.

Isaac invested $77,000 in an account paying interest rate of 4.6% compounded continuously.

This means that
`P(0) = 77000, r = 0.046`

Assuming no deposits or withdrawals are made, how much money, to the nearest cent, would be the count after 12 years?

This is P(12). So

`P(t) = P(0)e^(rt)`

`P(12) = 77000e^(0.046*12) = 133728`

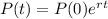
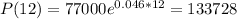
$133,728 would be in the count after 12 hours.