Question

25, 41, 49, 64Multiple ChoiceThe integers are not pairwise relatively prime since two of them have a common factor 3.The integers are pairwise relatively prime because there is no prime that divides all of them.The integers are pairwise relatively prime since two of them are prime.The integers are pairwise relatively prime because no two of them have a common prime factor.

Answer 1

The integers are pairwise relatively prime since two of them are prime

Explanation:

Given

`25, 41, 49, 64`

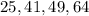
Required

Determine if they are prime factors

First, we determine the gcd of the 4 numbers

`25 = 1 * 5 * 5`

`41 =1 * 41`

`49 = 1 * 7 * 7`

`64 = 1 * 2 * 2 * 2 * 2 * 2 * 2`

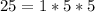
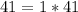
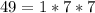
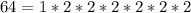
The common factor in the above computation is: 1

So:

`gcd = 1`

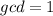
Because the gcd is 1, this implies that no prime divides all the given numbers.

Hence, they are pairwise relatively prime