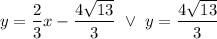Answer:
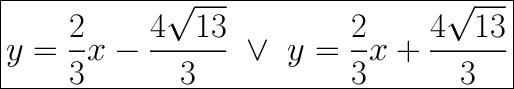
Explanation:
The equation of a line:
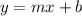
We have
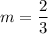
substitute:
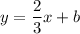
The formula of a distance between a point and a line:
General form of a line:
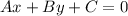
Point:
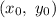
Distance:
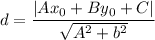
Convert the equation:
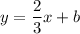 |subtract
|subtract
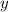 from both sides
from both sides
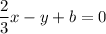 |multiply both sides by 3
|multiply both sides by 3
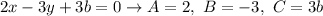
Coordinates of the point:
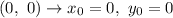
substitute:
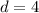
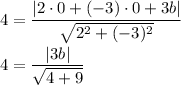
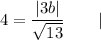 |multiply both sides by
|multiply both sides by
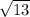
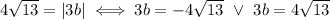 |divide both sides by 3
|divide both sides by 3
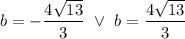
Finally: