Question

Circle A has center of (6, 7), and a radius of 4 and circle B has a center of (2, 4), and a radius of 16. What steps will help show that circle A is similar to circle B?

Answer 1

1) Use translation to coincide the center of a circle with the center of the other circle.

2) We construct the respective loci for the circles.

3) Compare each loci by direct inspection (
`f(x,y)` must be the same and radii must be different but constant) to conclude the similarity of the two circles.

Explanation:

Geometrically speaking, a circle is formed after knowing its center and radius.

1) Use translation to coincide the center of a circle with the center of the other circle. In this case, we translate the center (
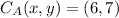`C_(A) (x,y) = (6,7)`) of the circle A to the location of the center of the circle B (
`C_(B)(x,y) = (2,4)`):

`C_(A') (x,y) = (6,7) + [(2,4) - (6,7)]`

`C_(A') (x,y) = (2,4)`

2) We construct the respective loci for the circles.

By Analytical Geometric, a circle is represented by the following locus:

`(x-h)^(2)+(y-k)^(2) = r^(2)`

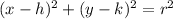
Where:

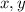`x, y` - Coordinates of a point of the circunference.

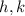`h, k` - Coordinates of the center of the circle.

`r` - Radius of the circle.

3) Compare each loci by direct inspection (
`f(x,y)` must be the same and radii must be different but constant) to conclude the similarity of the two circles.

Then, the circles A' and B are represented by the following loci:

Circle A'

`(x-2)^(2) + (y-4)^(2) = 16`

Circle B

`(x-2)^(2) + (y-4)^(2) = 256`

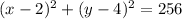
Since both the
`f(x,y)` component of each circle is the same and radii are different but constant, then we conclude that circle A is similar to circle B.