Question

All else being equal, if you cut the sample size in half, how does this affect the margin of error when using the sample

to make a statistical inference about the mean of the normally distributed population from which it was drawn?
zes
ME=
O The margin of error is multiplied by 0.5
O The margin of error is multiplied by a
O The margin of error is multiplied by 0.5.
O The margin of error is multiplied by 2.

Answer 1

The margin of error is multiplied by 4.

Explanation:

Margin of error is:

`M = (zs)/(√(n))`

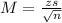
In which z is related to the confidence level, s is elated to the standard deviation and n is the sample size.

From this, we have that the standard deviation is inversely proportional to the square root of the sample size.

If you cut the sample size in half:

The margin of error is inversely proportional to the square root of the sample size, so if you cut the sample size by
`(1)/(2)`, the margin of error will be multiplied by
`2^2 = 4`

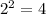
So

The margin of error is multiplied by 4.