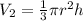Answer:
(b)
![V_2 = (\pi)/(4) [ ((2r)^2h)/(3)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/aznpzga0o0zhnf0moitvvkomluxnmnsll5.png) or
or
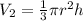
Explanation:
Given
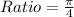
See attachment for complete question
Required
Determine the volume of the cone
The volume of a square pyramid is:
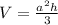
Where
a = base dimension
From the attachment, the base dimension of the square pyramid is 2r.
So:
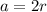
The volume becomes;
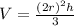
To calculate the volume of the cone, we simply multiply the given ratio and the volume of the prism.
So, we have:
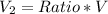
![V_2 = (\pi)/(4) [ ((2r)^2h)/(3)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/aznpzga0o0zhnf0moitvvkomluxnmnsll5.png)
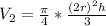
Open bracket;
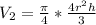
Cancel out 4
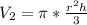
The above can be written as:
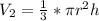
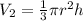
So, we have:
![V_2 = (\pi)/(4) [ ((2r)^2h)/(3)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/aznpzga0o0zhnf0moitvvkomluxnmnsll5.png)
or