Question

Differentiate the following functions (i) x(1+x)^3​

Answer 1

`\displaystyle y' = (1 + x)^2(4x + 1)`

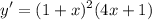
General Formulas and Concepts:

Algebra I

• Terms/Coefficients
• Functions
• Function Notation
• Factoring

Calculus

Derivatives

Derivative Notation

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Rule [Product Rule]:
`\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)`

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Step-by-step explanation:

Step 1: Define

Identify

y = x(1 + x)³

Step 2: Differentiate

1. Product Rule [Derivative Rule - Chain Rule]:
   `\displaystyle y' = (d)/(dx)[x] \cdot (1 + x)^3 + x \cdot (d)/(dx)[(1 + x)^3] \cdot (d)/(dx)[1 + x]`
2. Derivative Property [Addition/Subtraction]:
   `\displaystyle y' = (d)/(dx)[x] \cdot (1 + x)^3 + x \cdot (d)/(dx)[(1 + x)^3] \cdot ((d)/(dx)[1] + (d)/(dx)[x])`
3. Basic Power Rule:
   `\displaystyle y' = x^(1 - 1) \cdot (1 + x)^3 + x \cdot 3(1 + x)^(3 - 1) \cdot (0 + x^(1 - 1))`
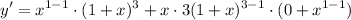
4. Simplify:
   `\displaystyle y' = (1 + x)^3 + 3x(1 + x)^2`
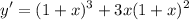
5. Factor:
   `\displaystyle y' = (1 + x)^2 \bigg[ (1 + x) + 3x \bigg]`
6. Combine like terms:
   `\displaystyle y' = (1 + x)^2(4x + 1)`

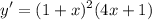
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Derivatives

Book: College Calculus 10e