Answer:
The 90% confidence interval, C.I = (0.693, 0.7307)
Explanation:
Catalysts 1 and catalyst 2 have the following statistical data;
Catalyst 1
The number of batches in the sample, n₁ = 12
The average yield by the 12 batches of catalyst 1,
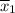 = 85
= 85
The sample standard deviation, s₁ = 4
Catalyst 2
The number of batches in the sample, n₂ = 10
The average yield,
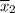 = 81
= 81
The standard deviation, s₂ = 5
F-test = s₂²/s₁² = 5²/4² = 1.5625
The degrees of freedom, df = n₁ + n₂ - 2
∴ df = 12 + 10 - 2 = 20
The critical-t at 90% confidence level = 1.725
The F-test < The critical-t, we pool the variance
The 90% confidence interval with the assumption of equal variance is given as follows;
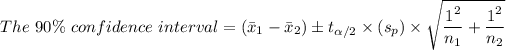
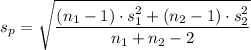
Therefore;
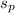 = √((12 - 1)×4² + (10 - 1)×5²)/(12 + 10 - 2)) ≈ 4.48
= √((12 - 1)×4² + (10 - 1)×5²)/(12 + 10 - 2)) ≈ 4.48
Therefore, we get;
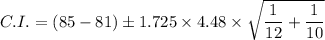
The 90% confidence interval, C.I = 0.693 < μ₁ - μ₂ < 7.307 = (0.693, 0.7307).