Question

How many distinct 3-letter permutations can you make from the letters in the word HEXAGON?

Answer 1

Answer: 210

===========================================================

Step-by-step explanation:

There are 7 unique letters in the word HEXAGON.

For the first slot, we have 7 choices. Then the next slot has 6 choices. Then the third slot has 5 choices. We count down by one each time we need to fill another slot.

Multiply out the values mentioned: 7*6*5 = 42*5 = 210

----------------

Alternatively, you can use the nPr permutation formula with n = 7 and r = 3.

`_n P _r = (n!)/((n-r)!)\\\\_7 P _3 = (7!)/((7-3)!)\\\\_7 P _3 = (7!)/(4!)\\\\_7 P _3 = (7*6*5*4*3*2*1)/(4*3*2*1)\\\\_7 P _3 = 7*6*5\\\\_7 P _3 = \boldsymbol{210}\\\\`

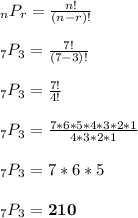
We have the "7*6*5" show up again after the "4*3*2*1" portions cancel.