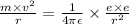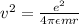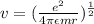Question

Consider an electron with charge −e−e and mass mmm orbiting in a circle around a hydrogen nucleus (a single proton) with charge +e+e. In the classical model, the electron orbits around the nucleus, being held in orbit by the electromagnetic interaction between itself and the protons in the nucleus, much like planets orbit around the sun, being held in orbit by their gravitational interaction. When the electron is in a circular orbit, it must meet the condition for circular motion: The magnitude of the net force toward the center, FcFcF_c, is equal to mv2/rmv2/r. Given these two pieces of information, deduce the velocity vvv of the electron as it orbits around the nucleus. Express your answer in terms of eee, mmm, rrr, and ϵ0ϵ0epsilon_0, the permittivity of free space.

Answer 1

Step-by-step explanation:

The net force on electron is electrostatic force between electron and proton in the nucleus .

Fc =
`(1)/(4\pi\epsilon) * (e* e)/(r^2)`

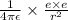
This provides the centripetal force for the circular path of electron around the nucleus .

Centripetal force required =
`(m* v^2)/(r)`

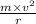
So

`(m* v^2)/(r)=(1)/(4\pi\epsilon) * (e* e)/(r^2)`

`v^2=(e^2)/(4\pi \epsilon m r)`

`v=((e^2)/(4\pi \epsilon m r))^{(1)/(2) }`