Question

`\displaystyle \rm\lim_(n \to \infty ) \sqrt[n]{ \left( \sum_(k = 1)^(n) \frac{ {k}^(2) }{ {2k}^(2) - 2nk + {n}^(2) } \right) \left( \sum_(k = 1)^(n) \frac{ {k}^3}{ {3k}^(2) - 3nk + {n}^(2) } \right)}`​ ​

Answer 1

Rewrite the sums as

`\displaystyle S_2 = \sum_(k=1)^n (k^2)/(2k^2 - 2nk + n^2) = \sum_(k=1)^n \frac{(k^2)/(n^2)}{(2k^2)/(n^2) - \frac{2k}n + 1}`

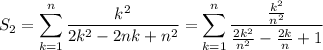
and

`\displaystyle S_3 = \sum_(k=1)^n (k^2)/(3k^2 - 3nk + n^2) = \sum_(k=1)^n \frac{(k^2)/(n^2)}{(3k^2)/(n^2) - \frac{3k}n + 1}`

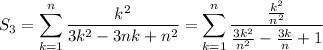
Now notice that

`\displaystyle \lim_(n\to\infty) \frac{S_2}n = \int_0^1 (x^2)/(2x^2 - 2x + 1) = \frac12`

and

`\displaystyle \lim_(n\to\infty) \frac{S_3}n = \int_0^1 (x^2)/(3x^2 - 3x + 1) = (9 + 2\pi\sqrt3)/(27)`

and the important point here is that
`\frac{S_2}n` and
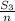`\frac{S_3}n` converge to constants. For any real constant a, we have

`\displaystyle \lim_(n\to\infty) \frac{\ln(an)}n = 0`

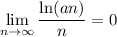
Rewrite the limit as

`\displaystyle \lim_(n\to\infty) \sqrt[n]{S_2 * S_3} = \lim_(n\to\infty) \exp\left(\ln\left(\sqrt[n]{S_2 * S_3}\right)\right) \\\\ = \exp\left(\lim_(n\to\infty) \frac{\ln(S_2) + \ln(S_3)}n\right) \\\\ = \exp\left(\lim_(n\to\infty) \frac{\ln\left(n * \frac{S_2}n\right) + \ln\left(n * \frac{S_3}n\right)}n\right)`

Then

`\displaystyle \lim_(n\to\infty) \sqrt[n]{S_2 * S_3} = e^0 = \boxed{1}`

A plot of the limand for n = first 1000 positive integers suggests the limit is correct, but convergence is slow.