Answer:
The answer is "4.3".
Explanation:
Given:
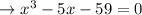
When


When
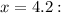
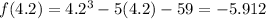
When
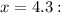
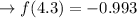 (closer to 0)
(closer to 0)

- It changes the sign so, the root lies in 4.3 and 4.4.
When
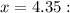
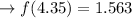
When the root is closer to 4.3 than 4.4 So, 1.563 is closer to zero than 4.184.
When
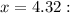
 close to zero.
close to zero.
So the answer is 4.3 to 1 decimal place.