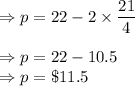Question

Find the profit-maximizing price.

80
For a monopolist's product, the demand equation is p = 22 - 2q and the average-cost function is c=2+
q
The profit-maximizing price is $


​

Answer 1

Answer:
`\$11.5`

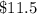
Explanation:

Given

Demand function is
`p=22-2q`

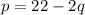
The average cost function is
`c=2+q`

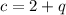
Total revenue is the product of demand and the price per unit.

`r=\left(22-2q\right)q`

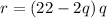
Profit is given by the difference of the total revenue and the cost

`\Rightarrow P=r-c\\\Rightarrow P=22q-2q^2-2-q\\\Rightarrow P=-2q^2+21q-2`

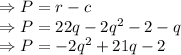
Find the derivative of profit to get the maximum profit

`\Rightarrow P'=-4q+21\\\text{Put the derivative equal to 0 to get the maximum profit}\\\\\Rightarrow q=(21)/(4)`

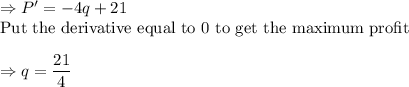
Put q in the equation of demand to get the price

`\Rightarrow p=22-2* (21)/(4)\\\\\Rightarrow p=22-10.5\\\Rightarrow p=\$11.5`