Question

A liquid dietary product implies in its advertising that use of the product for one month results in an average weight loss of at least three pounds. Eight subjects use the product for one month, and the resulting weight loss data are reported as follows.

Subject Initial Weight (lbs) Final Weight(lbs)
1 165 161
2 201 195
3 195 192
4 198 193
5 155 150
6 143 141
7 150 146
8 187 183
a) Do the data support the claim of the producer of the dietary product with the probability of Type 1 error of .05?
b) Do the data support the claim of the producer of the dietary product with the probability of Type 1 error of .01?
c) In an effort to improve sales, the producer is considering changing its claim from "at least three pounds" to "at least five pounds". Repeat parts a and b to test this new claim.

Answer 1

Following are the responses to the given question:

Explanation:

Please find the table in the attached file.

mean and standard deviation difference:
`\bar{d}=(\Sigma d)/(n) =(-4-6-.......-4-4)/(8)=-4.125 \\\\S_d=\sqrt{\frac{\Sigma (d-\bar{d})^2 }{n-1}}=\sqrt{((-4 + 4.125)^2 +.......+(-4 +4.125)^2 )/(8-1)}= 1.246`

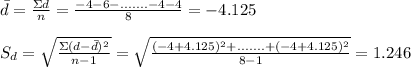
For point a:

hypotheses are:

`H_0 : \mu_d \geq -3\\\\H_a : \mu_d < -3\\\\`

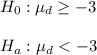
degree of freedom:

`df=n-1=8-1=7`

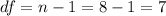
From t table, at
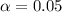`\alpha = 0.05`, reject null hypothesis if
`t <-1.895`.

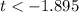test statistic:

`t=\frac{\bar{d}-\mu_d }{(s_d)/(√(d))}=( -4.125- (-3))/((1.246)/( √(8))) =-2.55`

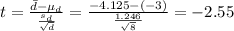
because the
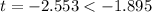`t=-2.553 <-1.895`, removing the null assumption. Data promotes a food product manufacturer's assertion with a likelihood of Type 1 error of 0.05.

For point b:

From t table, at
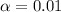`\alpha =0.01`, removing the null hypothesis if
`t<-2.998`.

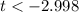because
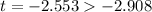`t=-2.553 >-2.908`, fail to removing the null hypothesis.

The data do not help the foodstuff producer's point with the likelihood of a .01-type mistake.

For point c:

Hypotheses are:

`H_0: \mu_d \geq -5\\\\H_a: \mu_d < -5`

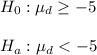
Degree of freedom:

`df=n-1=8-1=7`

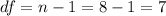
From t table, at
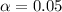`\alpha =0.05`, removing the null hypothesis if
`t <-1.895`.

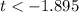test statistic:
`t=\frac{\bar{d}-\mu_d}{(s_d)/(√(n))} =(-4.125-(-5))/((1.246)/(√(8)))=1.986`

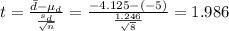
Since
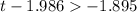`t-1.986 >-1.895`, The null hypothesis fails to reject. The results do not support the packaged food producer's claim with a Type 1 error probability of 0,05.

From t table, at
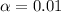`\alpha= 0.01`, reject null hypothesis if
`t<-2.998`.

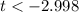Since
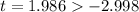`t=1.986>-2.998` , fail to reject null hypothesis.

Data do not support the claim of the producer of the dietary product with the probability of Type 1 error of .01.