Question

A student believes that the average grade on the statistics final examination was 87. A sample of 36 final examinations was taken. The average grade in the sample was 83.96 with a standard deviation of 12. The student wants to test whether the average is different from 87 at 90% level of confidence. Compute the p-value for this test.

Answer 1

The p-value for this test is 0.1375.

Explanation:

A student believes that the average grade on the statistics final examination was 87. The student wants to test whether the average is different from 87 at 90% level of confidence.

At the null hypothesis, we test if the average is 87, that is:

`H_0: \mu = 87`

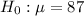
At the alternate hypothesis, we test if the average is different from 87, that is:

`H_a: \mu \\eq 87`

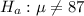
The test statistic is:

We have the standard deviation for the sample, which means that the t-distribution is used to solve this question.

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`s` is the standard deviation of the sample and n is the size of the sample.

87 is tested at the null hypothesis:

This means that
`\mu = 87`

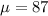
The average grade in the sample was 83.96 with a standard deviation of 12. Sample of 36

This means that
`X = 83.96, s = 12, n = 36`

Value of the test-statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (83.96 - 87)/((12)/(√(36)))`

`t = -1.52`

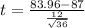
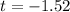
Pvalue:

Probability of the sample mean differing of 87, which means that we have a two-tailed test, with t = -1.52 and 36 - 1 = 35 degrees of freedom.

With the help of a calculator, the pvalue is of 0.1375.

The p-value for this test is 0.1375.