Question

The mean work week for engineers in start-up companies is claimed to be about 63 hours with a standard deviation of 5 hours. Kara, a newly hired engineer hopes that it's not (she wants it to be shorter). She asks 10 engineers in start-ups for the lengths of their mean work weeks. Their responses are 70; 45; 55; 60; 65; 55; 55; 60; 50; 55. a. Is the newly hired engineer testing a mean or a proportion? proportion mean b. The null hypothesis (or company claim), in symbols, is μ = . c. If the claim is correct, what is the probability that a sample mean would be as low as Kara's mean? % Give your answer as a percentage accurate to one decimal place. d. If Kara will accept the 63 hours as the real average so long as there's at least a 10% chance the sample average value could be as low as hers, should she accept the claim?

Answer 1

a. Mean

b. μ = μ₀

c. 11.5%

d. Yes

Explanation:

The given parameters are;

The mean work week for engineers, μ₀ = 63 hours

The standard deviation, σ = 5 hours

The number of engineers in Kara's sample, n = 10 engineers

The responses given by the 10 engineers are;

70; 45; 55; 60; 65; 55; 55; 60; 50; 55

a. The given information which the newly hired is hoping to find out that it is not is the mean

b. The null hypothesis which is that the company claim is correct, is therefore;

Null hypothesis, H₀; μ = μ₀ = 63 hours

c. Kara's mean,
`\overline x` is found as follows;

`\overline x` = (70 + 45 + 55 + 60 + 65 + 55 + 55 + 60 + 50 + 55)/10 = 57

`\overline x` = 57 hours

The Z-score is therefore;

`Z=(\overline x-\mu )/(\sigma )`

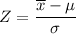
Z = (57 - 63)/5 = -1.2

From the Z-table, we have;

The p-value for P(
`\overline x` ≤ 57) = P(Z ≤ -1.2) = 0.11507

The probability as a percentage given to one decimal place, that the mean would be as low as Kara's mean, P(
`\overline x` ≤ 57) = 11.5%

d. Given that the percent percentage chance (11.5%) that the mean could be as low as hers (
`\overline x` = 57 hours) is higher than 10%, she should accept the claim.