Question

10.

Medical records at a doctor's office reveal that 12% of adult patients have seasonal
allergies. Select a random sample of 100 adult patients and let y = the number of
individuals in the sample who have allergies.

a) Calculate the mean and standard deviation of the sampling distribution of Y.

b) Interpret the standard deviation from part (a)

c) Would it be appropriate to use a normal distribution to model the sampling distribution of
Y? Justify your answer.
Math

Answer 1

a) The mean of Y is 12 and the standard deviation is 3.25.

b) The number of patients in the sample with seasonal allergies is expected to deviate from the mean by about 3.25.

c) Since
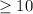`\\p \geq 10` and
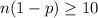`n(1-p) \geq 10`, it would be appropriate to use a normal distribution to model the sampling distribution of Y.

Explanation:

For each patient, there are only two possible outcomes. Either they have seasonal allergies, or they do not. The probability of a patient having seasonal allergies is independent of any other patient, which means that the binomial probability distribution is used to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

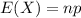
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

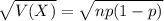
12% of adult patients have seasonal allergies.

This means that
`p = 0.12`

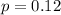
Sample of 100 adult patients

This means that
`n = 100`

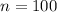
a) Calculate the mean and standard deviation of the sampling distribution of Y.

`E(Y) = np = 100*0.12 = 12`

`√(V(Y)) = √(np(1-p)) = √(100*0.12*0.88) = 3.25`

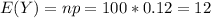
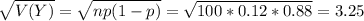
The mean of Y is 12 and the standard deviation is 3.25.

b) Interpret the standard deviation from part (a)

The number of patients in the sample with seasonal allergies is expected to deviate from the mean by about 3.25.

c) Would it be appropriate to use a normal distribution to model the sampling distribution of Y?

`np = 100*0.12 = 12 \geq 10`

`n(1-p) = 100*0.88 = 88 \geq 10`

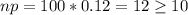
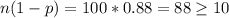
Since
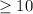`\\p \geq 10` and
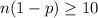`n(1-p) \geq 10`, it would be appropriate to use a normal distribution to model the sampling distribution of Y.