Question

A ball is dropped off a 700. m tall cliff, how long does it take to hit the ground?

Answer 1

`\boxed {\boxed {\sf 12.0 \ seconds}}`

Step-by-step explanation:

We are asked to find the time it tasked for a ball to hit the ground. We know the height, acceleration, and initial velocity, so we will use the following kinematic equation:

`d= v_i t + (1)/(2) at^2`

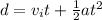
The ball starts at rest, so its initial velocity is 0 meters per second. The distance is 700 meters. The ball is in free fall, so the acceleration is due to gravity, or 9.8 meters per second squared.

• 
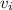  `v_i`= 0 m/s
• d= 700 m
• a= 9.8 m/s²

Substitute the values into the formula.

`700 \ m = (0 \ m/s)*t + (1)/(2) (9.8 \ m/s^2)t^2`

`700 \ m = (1)/(2) (9.8 \ m/s^2)t^2`

`700 \ m = 4.9 \ m/s^2 * t ^2`

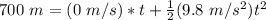
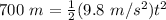
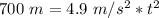
Divide both sides by 4.9 meters per second squared to isolate the variable t.

`\frac {700 \ m}{4.9 \ m/s^2}= (4.9 \ m/s^2*t^2)/(4/9 \ m/s^2)`

`\frac {700 \ m}{4.9 \ m/s^2}=t^2`

`142.857142857 \ s^2=t^2`

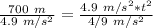
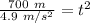
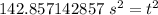
Take the square root of both sides.

`\sqrt {142.857142857 \ s^2} =\sqrt{t^2`

`11.9522860933 \ s = t`

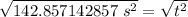
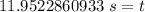
The original measurement has 3 significant figures, so our answer must have the same.

3 sig fig for our answer is the tenths place. The 5 in the tenths place tells us to round the 9 to a 0, then round the 1 to a 2.

`12.0 \ s = t`

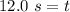
It takes the ball approximately 12.0 seconds to hit the ground.

Answer 2

Hi there!

We can use the kinematic equation:

d = v₀t + 1/2at²

d = displacement (m)

v₀ = initial velocity (0 m/s, dropped from rest)

t = time (s)

a = acceleration (due to gravity, 9.8 m/s²)

We can rearrange the equation to solve for time:

d = 1/2at²

2d = at²

t = √2d/a

Plug in the knowns. (a = g = 9.8 m/s²)

t = √2(700)(9.8) = 11.95 sec