1 Answer

Hajin · Answer 1 · 2022-03-18T14:05:57+0000

Given:

Number of students who has a cat and a dog = 5

Number of students who has a cat but do not have a dog = 11

Number of students who has a dog but do not have a cat = 3

Number of students who neither have a cat nor a dog = 2

To find:

The probability that a student has a cat given that they do not have a dog.

Solution:

Let the following events:

A = Student has a cat

B = Do not have a dog

Total number of outcomes is:

5+3+11+2=21

The probability that a student has a cat but do not have a dog is:

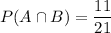
$P(A\cap B)=(11)/(21)$

The probability that a student do not have a dog is:

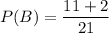
P(B)=(11+2)/(21)

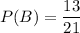
P(B)=(13)/(21)

The conditional probability is:

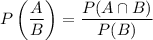
$P\left((A)/(B)\right)=(P(A\cap B))/(P(B))$

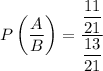
$P\left((A)/(B)\right)=((11)/(21))/((13)/(21))$

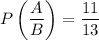
$P\left((A)/(B)\right)=(11)/(13)$

Therefore, the probability that a student has a cat given that they do not have a dog is
.

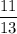Please log in or register to add a comment.