Question

The table represents...

Answer 1

D. b = 3

Explanation:

Given the following data;

Points on x-axis (x1, x2) = 10, 12

Points on y-axis (y1, y2) = 23, 27

First of all, we would determine the slope.

Mathematically, slope is given by the formula;

`Slope = (Change \; in \; y \; axis)/(Change \; in \; x \; axis)`

`Slope, m = \frac {y_(2) - y_(1)}{x_(2) - x_(1)}`

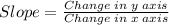
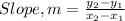
Substituting into the equation, we have;

`Slope, m = \frac {27 - 23}{12 - 10}`

`Slope, m = \frac {4}{2}`

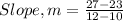
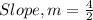
Slope, m = 2

The equation of straight line is y = mx + b

Where;

m is the slope.

x and y are the points

b is the intercept.

To find the intercept, we would use the following formula;

y - y1 = m(x - x1)

Substituting into the formula, we have;

y - 23 = 2(x - 10)

y - 23 = 2x - 20

y = 2x - 20 + 23

y = 2x + 3 = mx + b

Therefore, intercept, b = 3