Answer:
Horizontal translation in the
 direction.
direction.
Explanation:
A function of the form
 experiments an horizontal translation when the following substitution is applied:
experiments an horizontal translation when the following substitution is applied:
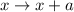 , where
, where
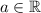
If
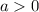 , the function is translated in the
, the function is translated in the
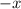 direction, whereas
direction, whereas
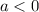 is the case for the function being translated in the
is the case for the function being translated in the
 direction.
direction.
The effect on the graph can be defined by a composition between two function:
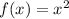 ,
,

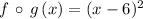
The resulting expression represents a horizontal translation in the
 direction.
direction.
Finally, we plot
 (red) and
(red) and
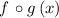 (blue) by a graphing tool and proved the certainty of this theory.
(blue) by a graphing tool and proved the certainty of this theory.