Question

Two people together can do a certain job in twenty minutes.If one of them can do the job alone in forty-five minutes, how long will the other person take to do the job alone?

Answer 1

36 minutes

Explanation:

Going through the question in bits:

i. Two people together can do a certain job in 20 minutes.

This implies that the time taken to finish the job is 20 minutes.

This also means that in 1 minute, they will do
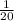`(1)/(20)` of the job i.e the rate at which the job is done by the two of them is
`(1)/(20)`

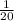
ii. If one of them can do the job in 45 minutes.

This implies that the time taken by one of them to finish the job is 45 minutes.

This also means that in 1 minute, he will do
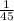`(1)/(45)` of the job. i.e the rate at which the job is done by one of them is
`(1)/(45)`

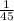
iii. let the other person do the job in x minutes.

This implies that the time take by the other person to finish the job is x minutes.

This also means that in 1 minute, he will do
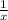`(1)/(x)` of the job. i.e the rate at which the job is done by the other person is
`(1)/(x)`

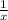
Now,

The rate by which the job will be done by the two of them combined is the sum of the individual rates.

i.e

`(1)/(20)` =
`(1)/(45)` +
`(1)/(x)`

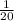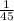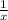
Multiply through by 90x and solve

(90x *
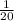`(1)/(20)`) = (90x *
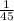`(1)/(45)`) + (90x *
`(1)/(x)`)

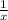4.5x = 2x + 90

4.5x - 2x = 90

2.5x = 90

x =
`(90)/(2.5)`

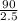
x = 36

Therefore it will take the other person 36 minutes to finish the job.