Question

Scientists are studying how the construction of a farm affects the blood diversity of insects in a forest before the Farm was constructed 186 insect species were present the scientist find out that after the farmers constructed the number of insect species decreased By 4% per month. Based on this trend which function could be used to calculate how many months, f(n) it Will take for the number of insect species to reach the value of N?

Answer 1

f(n)=log0.96(n/186)

Step-by-step explanation:

Answer 2

The function
`f(n)=log_(0.96)((n)/(186))`

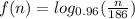
Step-by-step explanation:

Wherever we are studying logarithmic decrease or increase, we can construct our logarithmic function following the next recipe :

`f(n)=log_(x)((n)/(y))` (I)

Where
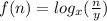`''n''` is the value that we want to obtain (following a logarithmic decrease or increase).

Where
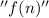`''f(n)''` is the time needed to obtain that variation.

Where
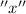`''x''` is the parameter related to the percentage decrease or increase

And where
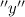`''y''` is known as the original population.

Now let's use the question to learn how to use the expression (I) :

In order to find the parameter
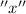`''x''` we need to know how porcentual the population changes. We know that the number of insect species decrease by 4 % per month.

Therefore, for the initial month we will have the 100 % of the number of insect species. For the first month we will have a decrease of 4 % which can be written as the 96 % of the original population.

We write 100 % - 4 % = 96 % ⇔
`1-0.04=0.96`

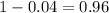
That's how we obtain the parameter
`x`. In this case we subtract 0.04 to the original population 1 because we have a decrease. Otherwise we would have added if we had had an increase. The number 0.96 represents that month by month we obtain the 96 % from the previous month. The value from the parameter is
`x=0.96`

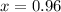
Now the original population of insect species is
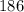`186`. Therefore the value for
`y` is
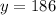`y=186`. Using the values obtained in the expression (i) we have :

`f(n)=log_(0.96)((n)/(186))`

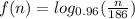
For example,

We have
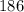`186` number of insect species at the time origin. A decrease of 4 % can be calculated as

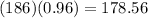`(186)(0.96)=178.56` which is the value expected for the first month. Now if we use this value in the expression (I) :

`n=178.56` ⇒
`f(178.56)=log_(0.96)((178.56)/(186))=log_(0.96)(0.96)=1` ⇒

`f(178.56)=1`

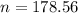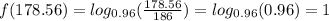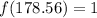
This means that to obtain 178.56 number of insect species we need to wait one month to achieve this value. Which fits with the problem data.