Answer:
(a) y =
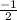 x -
x -
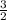
(b) y = 2x + 3
Explanation:
(a) The equation of a line given by points M(x₁, y₁) and N(x₂, y₂) is given by:
y - y₁ = m(x - x₁) -------------------(i)
Where;
m =
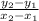 = slope or gradient of the line ---------------(ii)
= slope or gradient of the line ---------------(ii)
Given points on the triangle are:
A(2,5)
B(1,-2)
C(-5,1)
To find the equation of line BC, we use the formulas in equations (i) and (ii) where the points of the line are B(1,-2) and C(-5,1) and;
x₁ = 1
y₁ = -2
x₂ = -5
y₂ = 1
==> First get the gradient using equation (ii) as follows;
m =
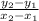 =
=
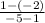
m =
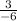
m =
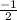
==> Now, use equation (i) to find the equation of the line as follows;
y - (-2) =
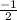 (x - 1)
(x - 1)
y + 2 =
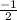 (x - 1)
(x - 1)
Multiply both sides by 2
2(y+2) = -1 ( x - 1 )
2y + 4 = -x + 1
2y = -x + 1 - 4
2y = - x - 3
y =
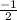 x -
x -
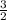
Therefore, the equation of the line is y =
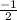 x -
x -
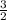
(b) To find the perpendicular line from A to BC, note that
i. two lines are perpendicular if they meet at 90°
ii. the general equation of a line could also be written as y = mx + c where m is the slope and c is the intercept.
iii. when one line has a slope of m, then a perpendicular line to that line will have a slope of

The equation of line BC is y =
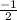 x -
x -
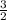 .
.
This means that BC has a slope of
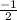
A perpendicular line from A to BC will have a slope of 2.
Now to get the equation of this perpendicular line from A(2, 5) to BC, we use the general equation of a line given in equation (i)
where;
m = 2
x₁ = 2
y₁ = 5
Substitute these values into equation (i)
y - 5 = 2(x - 2)
Solving by simplification gives;
y - 5 = 2x - 2
y = 2x + 3
Therefore, the equation of the perpendicular line is y = 2x + 3