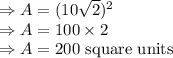Question

What is the biggest area of a quadrilateral you can fit in a circle that has a

circumference of 20π units? Show your work and a diagram to support your
answer

Answer 1

Answer: 200 square units

Explanation:

Given

Circumference of the circle is
`20\pi`

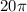
Suppose r is the radius of the circle

The biggest area of a quadrilateral that can fit in a circle is of square.

Deduce the radius of the circle

`2\pi r=20\pi\\r=10\ \text{units}`

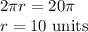
Suppose the side of the square is a

from the figure, we can write

`\Rightarrow a^2+a^2=(2r)^2\\\Rightarrow 2a^2=4r^2\\\Rightarrow a=√(2)r\\\Rightarrow a=10√(2)\ \text{units}`

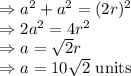
Area of the quadrilateral is

`\Rightarrow A=(10√(2))^2\\\Rightarrow A=100* 2\\\Rightarrow A=200\ \text{square units}`