Question

A researcher would like to estimate p, the proportion of U.S. adults who support recognizing civil unions between gay or lesbian couples.

If the researcher would like to be 95% sure that the obtained sample proportion would be within 1.5% of p (the proportion in the entire population of U.S. adults), what sample size should be used?
(a) 17,778
(b) 4,445
(c) 1,112
(d) 67
(e) 45
Due to a limited budget, the researcher obtained opinions from a random sample of only 2,222 U.S. adults. With this sample size, the researcher can be 95% confident that the obtained sample proportion will differ from the true proportion (p) by no more than (answers are rounded):
(a) .04%
(b) .75%
(c) 2.1%
(d) 3%
(e) There is no way to figure this out without knowing the actual sample proportion that was obtained.

Answer 1

Question 1:

(b) 4,445

Question 2:

(c) 2.1%

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

The margin of error is of:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

95% confidence level

So
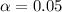`\alpha = 0.05`, z is the value of Z that has a pvalue of
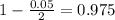`1 - (0.05)/(2) = 0.975`, so
`Z = 1.96`.

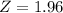Question 1:

We have no previous estimate for the population proportion, so we use
`\pi = 0.5`.

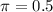The sample size is n for which M = 0.015. So

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`0.015 = 1.96\sqrt{(0.5*0.5)/(n)}`

`0.015√(n) = 1.96*0.5`

`√(n) = (1.96*0.5)/(0.015)`

`(√(n))^2 = ((1.96*0.5)/(0.015))^2`

`n = 4268`

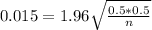
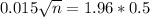
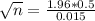
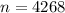
Samples above this value should be used, and the smaller sample above this value is of 4445, so the answer is given by option b.

Question 2:

Now we find M for which
`n = 2222`.

`M = z\sqrt{(\pi(1-\pi))/(n)}`

`M = 1.96\sqrt{(0.5*0.5)/(2222)}`

`M = 0.021`

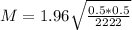
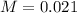
So 2.1%, and the correct answer is given by option c.