Question

(1) -3x-4y+11z from-9y+6z-3x
(2) 3x⁴-4x³+7x-2 from 9-7x⁴+6x³-2x²-11x​

Answer 1

1) 5y + 5z

2) 10x⁴ - 10x³ + 2x² + 18x - 11

Explanation:

Given the subtraction of the following polynomial expressions:

(1) -3x - 4y + 11z from -9y + 6z - 3x

In order to make it easier for us to perform the required mathematical operations, we must first rearrange the terms in the subtrahend by alphabetical order.

-3x - 4y + 11z

-3x - 9y + 6z ⇒ This is the subtrahend.

Now, we can finally perform the subtraction on both trinomials:

`\displaystyle\mathsf{\left \ \quad\:\:\:\:{-3x - 4y + 11z} \atop -\quad{\underline{-3x - 9y + 6z\:\:\underline}} \right.}`

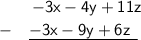
In the subtrahend, the coefficients of x and y are both negative. Thus, performing the subtraction operations on these coefficients transforms their sign into positive.

`\displaystyle\mathsf{\left \ \quad\:\:\:\:{-3x - 4y + 11z} \atop -\quad{\underline{-3x - 9y + 6z\:\:\underline}}\right.} \\\qquad\sf {\qquad\:\:\:0x\:+\:5y\:+5z`

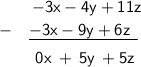
The difference is: 5y + 5z.

(2) 3x⁴- 4x³ + 7x - 2 from 9 - 7x⁴ + 6x³- 2x² - 11x​

Similar to the how we arranged the given trinomials in Question 1, we must rearrange the given polynomials in descending degree of terms before subtracting like terms.

3x⁴- 4x³ + 7x - 2 ⇒ Already in descending order (degree).

9 - 7x⁴ + 6x³- 2x² - 11x​ ⇒ -7x⁴ + 6x³- 2x² - 11x​ + 9

In subtracting polynomials, we can only subtract like terms, which are terms that have the same variables and exponents.

`\displaystyle\mathsf{\left \ \quad\:\:{3x^4\:-4x^3\:+\:0x^2\:+\:7x\:-\:2} \atop -\quad{\underline{-7x^4\:+6x^3\:-2x^2\:-11x\:+\:9 \:\:\underline}}\right.}`

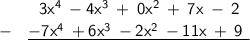
In the minuend, I added the "0x²" to make it less-confusing for us to perform the subtraction operations.

The same rules apply in terms of coefficients with negative signs in the subtrahend, such as: -7x⁴, - 2x², and - 11x​ ⇒ their coefficients turn into positive when performing subtraction.

`\displaystyle\mathsf{\left \ \quad\:\:{3x^4\:-4x^3\:+\:0x^2\:+\:7x\:-\:2} \atop -\quad{\underline{-7x^4\:+6x^3\:-2x^2\:-11x\:+\:9 \:\:\underline}}\right.} \\\qquad\sf {\qquad\:\:10x^4-10x^3+2x^2+18x\:-11`

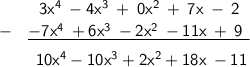
Therefore, the difference is: 10x⁴ - 10x³ + 2x² + 18x - 11.