Question

Maximum profit. A university student center sells 2,000 cups of coffee per day at a price of $4.0. A market survey shows that for every $0.1 reduction in price, 100 more cups of coffee will be sold. The cost of making one cup of coffee is $1.0. a) how much should the student center charge for a cup of coffee in order to maximize the profit? b) how many cups of coffee is the student center selling per day with this price? c) what is the maximum profit?

Answer 1

a) $3.50

b) 2,500 cups

c) $6,250

Explanation:

a) The number of cups of coffee the student sells, n = 2,000 cups

The price at which the student sells the coffee, P = $4.0

The number of extra cups sold for every $0.1 reduction in price = 100 cups

The cost of making one cup of coffee, C = $1.0

Let 'x' represent the set charge for a cup of coffee, we get;

The number of cups, nₙ = 2,000 + 100 × (4.0 - x)/0.1 = 6,000 - 1,000·x

Therefore, the revenue is given as follows;

Revenue, R = x × (6,000 - 1,000·x) = 6000·x - 1,000·x² = 1,000·(6·x - x²)

The cost, C = 1 × 6,000 - 1,000·x = 6,000 - 1,000·x

The profit, P = Revenue - Cost

∴ Profit = 6000·x - 1,000·x² - (6,000 - 1,000·x) = 7,000·x - 1,000·x² - 6,000

Profit, P = 7,000·x - 1,000·x² - 6,000 = 1,000 × (7·x - x² - 6)

At the maximum profit, we have; , we have;

dP/dx = 0

∴ dP/dx = d(1,000 × (7·x - x² - 6))/d

dR/dx = 1,000·d(7·x - x² - 6)/dx = 1,000 × (7 - 2·x) = 0

x = 7/2 = 3.5

The price that gives the maximum profit, x = $3.50

Therefore, the amount the student center should charge for a cup of coffee to maximize profit, x = $3.50

b) We have;

The number of cups, n = 6,000 - 1,000 × 3.5 = 2,500

The number of cups of coffee the student center sells at the price that gives the maximum profit, n = 2,500 cups

c) The maximum profit,
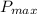`P_(max)` = 1,000 × (7 × 3.5 - 3.5² - 6) = 6,250

The maximum profit,
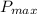`P_(max)` = $6,250.