Question

During an extremely foggy day during the medieval era, an architect wants to determine the height of a building. He cannot see to the top of his building, but he stands on the roof and lowers a pendulum to the ground. If the pendulum swings with a period of 12 seconds, what is the height of the building?

Answer 1

Height of the building = 35.78 m

Step-by-step explanation:

Given that,

The time period of a pendulum is, T = 12 s

We need to find the height of the building. The formula for the time period of a pendulum is given by :

`T=2\pi \sqrt{(l)/(g)}`

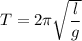
Where

l is the height of the building

`l=(T^2g)/(4\pi^2)\\\\l=((12)^2* 9.8)/(4* 3.14^2)\\\\l=35.78\ m`

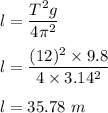
So, the height of the building is 35.78 m.