Question

#5: The population of a certain animal species decreases at a rate of 2.5%. If there are 400 of this animal in the wild, using an exponential function, predict approximately how many there will be in 4 years. Round to the nearest whole number. *

Answer 1

There will be 361 individuals in 4 years.

Explanation:

Exponential equation of population decay:

The amount of individuals of a certain population, after t years, with a decay rate of r(as a decimal), is given by:

`A(t) = A(0)(1-r)^t`

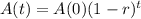
In which A(0) is the initial population and r is the decay rate.

The population of a certain animal species decreases at a rate of 2.5%.

This means that
`r = 0.025`

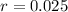
There are 400 individuals:

This means that
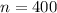`n = 400`. So

`A(t) = A(0)(1-r)^t`

`A(t) = 400(1-0.025)^t`

`A(t) = 400(0.975)^t`

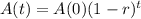
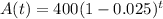
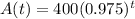
How many there will be in 4 years?

This is A(4). So

`A(4) = 400(0.975)^4 = 361.4`

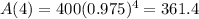
Rounding to the nearest whole number, there will be 361 individuals in 4 years.