Question

An astronaut is a distance L from her spaceship, and is at rest with respect to the ship, when she discovers that her tether has broken. She tosses a wrench with a speed Vw in the opposite direction of the ship to propel herself back to the ship. The astronaut has mass MA, and the wrench has mass Mw.

Required:
a. Draw a sketch, showing the subsequent motion of the astronaut and the wrench.
b. What is the initial momentum (before toss) of the astronaut plus wrench system? What is the final momentum?
c. Use conservation of momentum to solve for the speed of the astronaut VA, relative to the ship, in terms of MA, Mw and Vw.
d. How long does it take her to reach the ship in terms of L, MA, Mw and Vw?
e. How far has the wrench traveled from its original position when the astronaut reaches the ship? Express your answer in terms of L, MA and Mw.

Answer 1

B) I₀ = I_f= 0, C) vₐ =
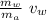`(m_w)/(m_a) \ v_w` , D) t =
`(m_a)/(m_w) \ (L)/(v_w)`

Step-by-step explanation:

A) in the attachment you can see a diagram of the movement of the key and the astronaut that is in the opposite direction to each other.

B) Momentum equals the change in momentum in the system

I = ∫ F dt = Δp

since the astronaut has not thrown the key, the force is zero, so the initial impulse is zero

I₀ = 0

The final impulse of the two is still zero, since it is a vector quantity, subtracting the impulse of the two gives zero, since it is an isolated system

I_f = 0

C) We define the system formed by the astronaut and the key, for which the forces during the separation are internal and the moment is conserved

initial instant.

p₀ = 0

final instant

p_f =
`m_a v_a - m_w v_w`

We used the subscript “a” for the astronaut and the subscript “w” for the key

the moment is preserved

po = p_f

0 = mₐ vₐ - m_w v_w

vₐ =
`(m_w)/(m_a) \ v_w`

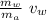
D) as the astronaut goes at constant speed we can use the uniform motion relationships

vₐ = x / t

t = x / vₐ

t =
`(m_a)/(m_w) \ (L)/(v_w)`