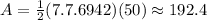Question

Identify the area of a regular decagon with side length 5 m rounded to the nearest tenth.

THE RED IS THE ONE I GOT WRONG

Answer 1

192.4 m^2

Explanation:

See the attached image.

The area of a regular polygon is
`A=(1)/(2)ap` where p is the perimeter and a is the apothem (the distance from the center to the midpoint of a side).

The perimeter is p = 10(5) = 50m. This is a huge decagon!

Calculate the measure of angle KGL. In a decagon, the total of all interior angles is 180(10-2) = 1440 degrees. That makes one of the interior angles 1440 / 10 = 144, and angle KGL is half of that, 72 degrees.

To find a, use a trigonometric ratio in right triangle GKL. GL = 2.5, half the length of side GH.

`tan(72^\circ) = a/2.5\\\\a=2.5tan(72^\circ) \approx 7.6942`

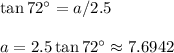
The area of the decagon is

`A=(1)/(2)(7.7.6942)(50) \approx 192.4`