A possible starting point:
Split up the limit as
![\displaystyle \lim_(n\to\infty) \frac{1 + \sqrt[3]{2} + \cdots + \sqrt[3]{n}}{n^(4/3)} * \lim_(n\to\infty) \frac1{n \left(\frac1{(an+1)^2} + \frac1{(an+2)^2} + \cdots + \frac1{(an+n)^2}\right)} = 54](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/5a3layobxm7bfveyjcm3.png)
Consider the first limit,
![\displaystyle \lim_(n\to\infty) \frac{1 + \sqrt[3]{2} + \cdots + \sqrt[3]{n}}{n^(4/3)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/dwigs8hkgcg49ppqyxhe.png)
Refer to the Stolz-Cesàro theorem, which says
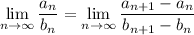
where
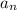 and
and
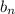 are two real sequences, with
are two real sequences, with
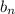 monotone and divergent. In this case,
monotone and divergent. In this case,
![a_n = 1+\sqrt[3]{2}+\sqrt[3]{3}+\cdots+\sqrt[3]{n}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/2inrt9kdqeitfqwd81ad.png)
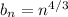
Applying S-C, we get
![\displaystyle \lim_(n\to\infty) \frac{\sqrt[3]{n+1}}{(n+1)^(4/3) - n^(4/3)} = \lim_(n\to\infty) ((n+1)^(1/3))/((n+1)^(4/3) - n^(4/3))](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/lz0sz2qq784f6hw8vbf2.png)
Recalling the difference of cubes identity,
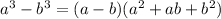
we can rewrite the limit as
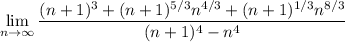
and dividing uniformly through the limand by (n + 1)³ yields

Now,
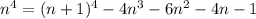
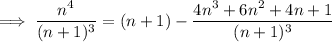
so the denominator in the limit reduces to a degree-1 polynomial with leading coefficient +4. The numerator converges to 1 + 1 + 1 = 3, so this first limit evaluates to
![\displaystyle \lim_(n\to\infty) \frac{1 + \sqrt[3]{2} + \cdots + \sqrt[3]{n}}{n^(4/3)} = \frac34](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ah1f7pupxze6h6z03c59.png)
It remains to determine the value of a such that
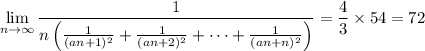
We have a natural choice of lower and upper bounds for the sum in the denominator:
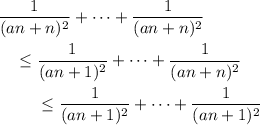

and
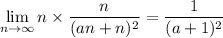
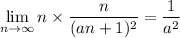
so that by the squeeze/sandwich theorem,
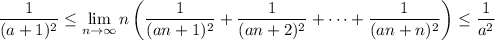
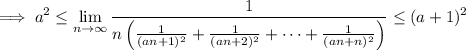
and if the middle limit is supposed to evaluate to 72, solving the inequality for a puts it in the interval [6√2 - 1, 6√2] ≈ [7.48528, 8.48528].
Checking against a computer, the solution appears to be a = 8, which agrees with the analysis above. Just not sure how to bridge the gap yet...