Question

A. Their rates of change differ by 2. B. Their rates of change differ by 4. C. Function M has a greater rate of change than Function P. D. Function M and Function P have the same rate of change.

Answer 1

(a) Their rates of change differ by 2

Explanation:

Given

See attachment for functions M and P

Required

Determine what is true about the rates of M and P

First, we calculate the slope (i.e. rate) of both functions.

Slope is calculated as:

`m = (y_2 -y_1)/(x_2 - x_1)`

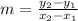
From the table of M, we have:

`(x_1,y_1) = (-2,-9)`

`(x_2,y_2) = (2,11)`

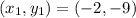
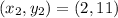
So, the slope is:

`m_M = (11 --9)/(2--2)`

`m_M = (20)/(4)`

`m_M = 5`

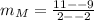
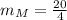
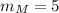
For function P, we have:

`y = 7x + 9`

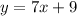
A function is represented as:

`y = mx + b`

Where:

`m = slope`

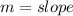
So, by comparison:

`m_P = 7`

At this point, we have:

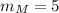`m_M = 5` --- Slope of M

`m_P = 7` --- Slope of P

Only option (a) is true because both slopes differ by 2. i.e. 7 - 5 = 2

Other options are not true