Question

Log x + log (x-3) = 1

Answer 1

Given:

The logarithmic equation is:

`\log x+\log (x-3)=1`

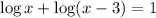
To find:

The value of x.

Solution:

Properties of logarithm used:

`\log a+\log b=\log (ab)`

`\log 10=1`

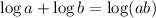
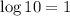
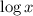`\log x` is defined for
`x>0`.

We have,

`\log x+\log (x-3)=1`

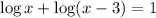
Using properties of logarithm, we get

`\log [x(x-3)]=\log 10`

`x^2-3x=10`

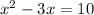
Splitting the middle term, we get

`x^2-5x+2x-10=0`

`x(x-5)+2(x-5)=0`

`(x-5)(x+2)=0`

`x=5,-2`

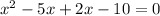
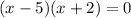
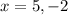
In the given equation, we have a term
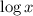`\log x`. It means the value of x must be greater than 0 or positive. So, the only possible value of x is:

`x=5`

Therefore, the value of x is 5.