Question

A random sample of 30 males with online dating profiles are recruited for a study about lying in online dating profiles. Each male's actual height is measured and compared to the height posted in their online profile. The difference between the online profile height and the actual height (profile- actual) for each male is computed. The mean difference in height is determined to be 0.57 inches with a standard deviation of 0.81 inches. Determine a 95% confidence interval for the difference in mean profile height and mean actual height of online daters.

Answer 1

Given the provided data, the confidence interval is estimated to be between -0.324 inches and 1.224 inches, with 95% confidence.

Step-by-step explanation:

To determine a 95% confidence interval for the difference in mean profile height and mean actual height of online daters, we can use the formula:

Confidence interval = mean difference ± (critical value * standard deviation / sqrt(sample size))

Given that the mean difference is 0.57 inches, the standard deviation is 0.81 inches, and the sample size is 30, we need to find the critical value for a 95% confidence level.

This critical value corresponds to the z-score for a 95% confidence level, which is approximately 1.96.

Plugging in the values, the confidence interval is:

`0.57 +/- (1.96 * 0.81 / \sqrt{(30))`

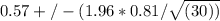
Calculating this, the lower bound of the confidence interval is approximately -0.324 and the upper bound is approximately 1.224. Therefore, with 95% confidence, the difference in mean profile height and mean actual height of online daters is estimated to be between -0.324 inches and 1.224 inches.

Answer 2

The 95% confidence interval for the difference in mean profile height and mean actual height of online daters is between 0.27 and 0.87 inches.

Step-by-step explanation:

We have the standard deviation for the sample, which means that the t-distribution is used to solve this question.

The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So

df = 30 - 1 = 29

95% confidence interval

Now, we have to find a value of T, which is found looking at the t table, with 29 degrees of freedom(y-axis) and a confidence level of
`1 - (1 - 0.95)/(2) = 0.975`. So we have T = 2.0452

The margin of error is:

`M = T(s)/(√(n)) = 2.0452(0.81)/(√(30)) = 0.3`

In which s is the standard deviation of the sample and n is the size of the sample.

The lower end of the interval is the sample mean subtracted by M. So it is 0.57 - 0.3 = 0.27 inches.

The upper end of the interval is the sample mean added to M. So it is 0.57 + 0.3 = 0.87 inches.

The 95% confidence interval for the difference in mean profile height and mean actual height of online daters is between 0.27 and 0.87 inches.