Question

Solve the trigonometric function
tan∅ × sin∅ × cos∅ + cos2∅

Answer 1

cos²Θ

Explanation:

simplify the expression using the identities

tanΘ =
`(sin0)/(cos0)`

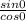
cos2Θ = 1 - 2sin²Θ

cos²Θ = 1 - sin²Θ

then

tanΘ × sinΘ × cosΘ + cos2Θ

=
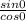`(sin0)/(cos0)` × sinΘ × cosΘ + 1 - 2sin²Θ ( cancel cosΘ on numerator/ denominator )

= sinΘ × sinΘ + 1 - 2sin²Θ

= sin²Θ + 1 - 2sin²Θ

= 1 - sin²Θ

= cos²Θ

Answer 2

`\cos^2(\theta)`

Explanation:

Trig identities used:

`\cos(2\theta)=\cos^2(\theta)-\sin^2(\theta)`

`\tan(\theta)=(\sin(\theta))/(\cos(\theta))`

Therefore,

`\tan(\theta)*\sin(\theta)*\cos(\theta)+\cos(2\theta)`

`=(\sin(\theta))/(\cos(\theta))*\sin(\theta)*\cos(\theta)+\cos(2\theta)`

`=\sin^2(\theta) +\cos(2\theta)`

`=\sin^2(\theta) +\cos^2(\theta)-\sin^2(\theta)`

`=\cos^2(\theta)`