Answer:

Explanation:
This problem must be solved using the midpoint formula, which is similar to a slope formula.
Midpoint formula:
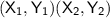
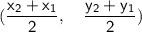
y2=(-6)
y1=(-1)
x2=(-1)
x1=(-6)
Rewrite the problem and then solve it.

Dividing is another option.
-7/2=-3.5
(-3.5, -3.5)
As a result, the final answer is (-3.5, -3.5).
I hope this helps! Let me know if my answer is wrong or not.