Question

2. [5pts] The Pew Research Group conducted a poll in which they asked, "Are you in favor of, or opposed to, executing persons as a general policy when the crime committed while under the age of 18?" Of the 580 Catholics surveyed, 180 indicated they favored capital punishment; of the 600 seculars surveyed, 238 favored capital punishment. Is there a significant difference in the proportion of individuals in these groups in favor of capital punishment for persons under the age of 18? Use the ???? = 0.01 level of significance. Show all work.

Answer 1

See below for answers and explanations

Explanation:

Here, we are comparing two proportions of a large sample size. Therefore, conducting a 2-proportion z-test is appropriate. Conditions are already assumed, so we can conduct the test.

We are testing our null and alternate hypotheses which are:

H: p1=p2 (there is no difference)

Ha: p1≠p2 (there is a difference)

Given:

x1=180

n1=580

x2=238

n2=600

p1=180/580=0.31

p2=238/600=0.4

p=(180+238)/(580+600)=418/1180=0.35

Use the formula to calculate the z-statistic:

`Z=\frac{p_1-p_2}{\sqrt{p(1-p)((1)/(n_1)+(1)/(n_2))}}`

`Z=\frac{0.31-0.4}{\sqrt{0.35(1-0.35)((1)/(580)+(1)/(600))}}`

`Z=-3.24`

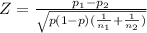
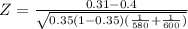
Calculate p-value (note that this is two-sided):

1) normalcdf(-1e99,-3.24)=5.977105194*10^-4

2) Since this is a two-sided test, we double it to get p=0.001195421

Conclusion: Since 0.0012<0.05, we reject the null hypothesis and conclude that there is a significant difference in the proportion of individuals in these groups in favor of capital punishment for persons under the age of 18 because our p-value is extremely low.