Question

A 37.2 g sample of copper at 99.8 °C is carefully placed into an insulated container containing 188 g of water at 18.5 °C. Calculate the final temperature when thermal equilibrium is reached. Assume there is no energy transferred to or from the container. Specific heat capacities: Cu = 0.385 J g-1 °C-1 H2O = 4.184 J g-1 °C-1

Answer 1

T₂ = 19.95°C

Step-by-step explanation:

From the law of conservation of energy:

`Heat\ Lost\ by\ Copper = Heat\ Gained\ by\ Water\\m_cC_c\Delta T_c = m_wC_w\Delta T_w`

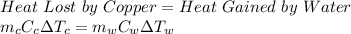
where,

mc = mass of copper = 37.2 g

Cc = specific heat of copper = 0.385 J/g.°C

mw = mass of water = 188 g

Cw = specific heat of water = 4.184 J/g.°C

ΔTc = Change in temperature of copper = 99.8°C - T₂

ΔTw = Change in temperature of water = T₂ - 18.5°C

T₂ = Final Temperature at Equilibrium = ?

Therefore,

`(37.2\ g)(0.385\ J/g.^oC)(99.8\ ^oC-T_2)=(188\ g)(4.184\ J/g.^oC)(T_2-18.5\ ^oC)\\99.8\ ^oC-T_2 = ((188\ g)(4.184\ J/g.^oC))/((37.2\ g)(0.385\ J/g.^oC))(T_2-18.5\ ^oC)\\\\99.8\ ^oC-T_2 = (54.92) (T_2-18.5\ ^oC)\\54.92T_2+T_2 = 99.8\ ^oC + 1016.02\ ^oC\\\\T_2 = (1115.82\ ^oC)/(55.92)`

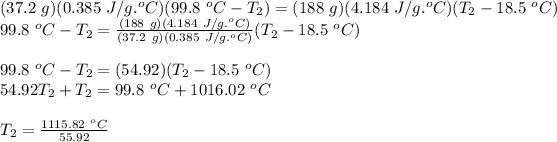
T₂ = 19.95°C