Question

A company that makes cola drinks states that the mean caffeine content per​ 12-ounce bottle of cola is 35 milligrams. You want to test this claim. During your​ tests, you find that a random sample of thirty​ 12-ounce bottles of cola has a mean caffeine content of 36.8 milligrams. Assume the population is normally distributed and the population standard deviation is 7.3 milligrams. At α=0.02​, can you reject the​ company's claim? Complete parts​ (a) through​ (e).

Answer 1

The pvalue of the test is 0.177 > 0.02, which means that at α=0.02, you cannot reject the company's claim.

Explanation:

A company that makes cola drinks states that the mean caffeine content per​ 12-ounce bottle of cola is 35 milligrams. You want to test this claim.

At the null hypothesis, you test that the mean caffeine content is of 35 milligrams, that is:

`H_o: \mu = 35`

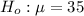
And at the alternate hypothesis, you test if the content is different from 35, so:

`H_a: \mu \\eq 35`

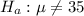
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

35 is tested at the null hypothesis:

This means that
`\mu = 35`

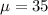
During your​ tests, you find that a random sample of thirty​ 12-ounce bottles of cola has a mean caffeine content of 36.8 milligrams. Assume the population is normally distributed and the population standard deviation is 7.3 milligrams.

This means that
`n = 30, X = 36.8, \sigma = 7.3`

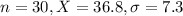
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (36.8 - 35)/((7.3)/(√(30)))`

`z = 1.35`

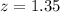
Pvalue of the test and decision:

The pvalue of the test is the probability of the mean caffeine content differing from the mean by at least 36.8 - 35 = 1.8, which is P(|z| > 1.35), which is 2 multiplied by the pvalue of z = -1.35.

Looking at the z = -1.35 has a pvalue of 0.0885

2*0.0885 = 0.177

The pvalue of the test is 0.177 > 0.02, which means that at α=0.02, you cannot reject the company's claim.