Question

Conduct the following test at the level of significance by determining ​(a) the null and alternative​ hypotheses, ​(b) the test​ statistic, and​ (c) the​ P-value. Assume that the samples were obtained independently using simple random sampling. Test whether . Sample data are ​, ​, ​, and . ​(a) Determine the null and alternative hypotheses. Choose the correct answer below. A. versus B. versus C. versus Your answer is correct.D. versus ​(b) The test statistic is nothing. ​(Round to two decimal places as​ needed.)

Answer 1

Hello your question is poorly written the complete question is attached below

answer :

a) H0 : p1 = p2

Ha : p1 ≠ p2

b) Z = -0.58

c) P-value = 0.561915

d) we will reject the Alternative hypothesis

Explanation:

For sample 1 ; n1 = 254 , x1 = 28

For sample 2 ; n2 = 301 , x2 = 38

level of significance ∝ = 0.01

P1 = X1 / n1 = 28 / 254 = 0.1102

P2 = X2 / n2 = 38 / 301 = 0.126

a) Determine the null and alternate hypothesis

H0 : p1 = p2

Ha : p1 ≠ p2

b) Determine Test statistic

we perform a Z-statistic to test the hypothesis

Z =
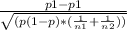`\frac{p1-p1 }{\sqrt{( p(1-p)*((1)/(n1)+(1)/(n2)) ) } }` -------- ( 1 )

p = ( x1 + x2 ) / ( n1 + n2 )

= ( 28 + 38 ) / ( 254 + 301 ) = 0.1189

Where: p = 0.1189 , p1 = 0.1102 , p2 = 0.126 ( input values into equation 1 )

∴ Z = -0.58

c) Determine P-value

P-value = 0.561915 ( using excel function )

d) conclusion : since p-value > 0.01 ( level of significance ) we do not reject the null hypothesis. therefore it proves that p1 = p2