Question

A light bulb manufacturer guarantees that the mean life of a certain type of light bulb is at least 754 hours. A random sample of 29 light bulbs has a mean life of 737 hours. Assume the population is normally distributed and the population standard deviation is 59 hours. At α=0.08​, do you have enough evidence to reject the​ manufacturer's claim? Complete parts​ (a) through​ (e)

Answer 1

The calculated test |Z| = |-1.55| >1.405 at 0.08 level of significance

The null hypothesis is rejected at a 0.08 level of significance.

An Alternative hypothesis is accepted

A light bulb manufacturer guarantees that the mean life of a certain type of light bulb is at most 754 hour

Explanation:

Step(i):-

Given that the mean life of a certain type of light bulb is at least 754 hours

Given that the random sample size 'n' =29

Given that the mean life of sample x⁻ = 737

Given that the standard deviation of the Population = 59

Step(ii):-

Null hypothesis: H₀: μ≥ 754

Alternative Hypothesis:H₁: μ≤ 754

Test statistic

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

`Z = (737-754 )/((59)/(√(29) ) )`

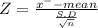
Z = -1.55

The calculated test |Z| = |-1.55| >1.405 at 0.08 level of significance

The null hypothesis is rejected at 0.08 level of significance

Final answer:-

The calculated test |Z| = |-1.55| >1.405 at 0.08 level of significance

The null hypothesis is rejected at a 0.08 level of significance.

A light bulb manufacturer guarantees that the mean life of a certain type of light bulb is at most 754 hour