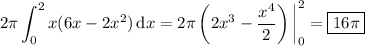Question

Use the method of cylidrincal shells to find the volume of the solid generated by rotating the region bounded by the curves y=6x-2x^2 and y=x^2 about the y axis.

Answer 1

Find where the two curves intersect:

y = 6x - 2x ²

y = x ²

6x - 2x ² = x ² → 3x ² - 6x = 3x (x - 2) = 0 → x = 0 and x = 2

Now, for a shell of radius x units away from the axis of revolution, the height of the shell would be the vertical distance between the upper curve and the lower curve. For 0 ≤ x ≤ 2, we have 6x - x ² ≥ x ², so the height of any given shell is (6x - x ²) - x ² = 6x - 2x ².

Then volume of the solid is

`\displaystyle 2\pi \int_0^2 x(6x-2x^2)\,\mathrm dx = 2\pi \left(2x^3-\frac{x^4}2\right)\bigg|_0^2 = \boxed{16\pi}`