1 Answer

Framp · Answer 1 · 2022-11-11T00:34:28+0000

Given:

The equation of the curve is:

$y=x^{(5)/(2)}$

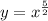
To find:

The gradient of the given curve at the point where
x = 4 .

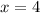Solution:

We have,

$y=x^{(5)/(2)}$

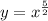
Differentiate with respect to x.

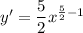
$y'=(5)/(2)x^{(5)/(2)-1}$
$[\because (d)/(dx)x^n=nx^(n-1)]$

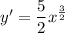
$y'=(5)/(2)x^{(3)/(2)}$

Substituting
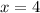x=4 , we get

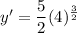
$y'=(5)/(2)(4)^{(3)/(2)}$

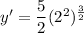
$y'=(5)/(2)(2^2)^{(3)/(2)}$

Using properties of exponents, we get

$y'=(5)/(2)(2)^{2* (3)/(2)}$
$[\because (a^m)^n=a^(mn)]$

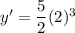
y'=(5)/(2)(2)^(3)

y'=(5)/(2)(8)

y'=20

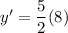
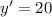
Therefore, the gradient of the given curve at the point where
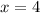is 20.

Please log in or register to add a comment.