Answer:
The projectile will hit the ground after 38.8 seconds.
Explanation:
You know that the height s (t) in feet of the projectile after t seconds is given by the function
s(t) = - 16t² + 600t + 800.
To know the time at which the projectile will hit the ground, you must replace s(t) by height 0:
0=- 16t² + 600t + 800
This is a quadratic function of the form ax2 + bx + c, where a= -16, b=600 and c=800.
To solve a quadratic function, you must apply the expression:
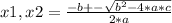
In this case:

Solving:
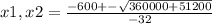

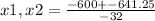
So:
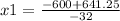
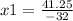
x1= -1.289 seconds
and
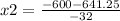

x2= 38.789 ≅ 38.8 seconds
Time cannot be negative. So, the projectile will hit the ground after 38.8 seconds.