Question

Question 7: Find the value of x. The numbers below are in degrees.

140
S
50
20

Answer 1

Given:

A figure.

To find:

The value of x.

Solution:

Draw two parallel lines as shown in the below figure.

If a transversal line intersect two parallel lines, then alternate interior angles are same.

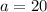`a=20` (Alternate interior angle)

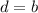`d=b` (Alternate interior angle) ...(i)

The value of angle d is

`d=50-a`

`d=50-20`

`d=30`

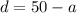
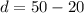
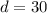
Using (i), we get

`b=30`

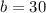
If a transversal line intersect two parallel lines, then same sides interior angles are supplementary angles.

`c+140=180`

`c=180-140`

`c=40`

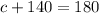
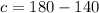
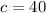
Now,

`x=b+c`

`x=30+40`

`x=70`

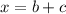
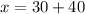
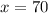
Therefore, the value of x is 70.