Question

An arm wrestler is the champion for a period of 75 hours. (Here, by an hour, we mean a period starting from an exact hour, such as 1 P.M., until the next hour.) The arm wrestler had at least one match an hour, but no more than 125 total matches. Show that there is a period of consecutive hours during which the arm wrestler had exactly 24 matches.

Answer 1

The answer is "In the i-th to J-th hour, the Wrestler played only 24 match-ups".

Explanation:

Let
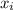`x_i` label the number of teams played by the wrestler for
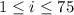`1 \leq i \leq 75`, after i-th hour, where
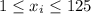`1 \leq x_i \leq 125`. This also means
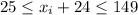`25 \leq x_i + 24 \leq 149`. The Pigeonhole Principle means that
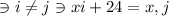`\\i i \\eq j \\i x i+ 24 = x ,j` is played exactly 24 matches between the i-th and j-th-hours end. Thus, 150 integrals
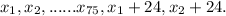`x_1,x_2,......x_(75), x_1+24,x_2+24.` In the i-th to J-th hour, the Wrestler played only 24 match-ups.